addition 을 구현 하기 위해서는 carry 와 sum 을 구현해야 한다.
이때에 carry 는 더해지는 연산자가 a, b 라고 할때에 carry = ab, sum = a xor b 로 나타낼 수 있다.
이를 한자리 수 덧셉에만 적용하지 않고 더 나아가서 두자리 덧셈에서도 활용 할 수 있다.

위와 같이 두자리수 덧셈에 대해서 한 테이블에 모두 나타낼 수 있다. 이렇게 만든다면, 각각의 값에 대해서 즉각적으로 결과 값을 만들어 낼 수 있다. 하지만 차지 하는 공간이 자릿수가 늘수록 커진다. 또한 필요한 트렌지스터의 개수가 늘어나게 된다. 이는 truth-table의 크기와 비례하기 때문에 truth-table의 크기에 대해 생각해 본다면 4bit half adder의 경우 입력 값이 chd 8bit 이므로 행의 계수가 2 ^ 8이다.
이를 circit 으로 구현 하면 아래와 같이 표현 할 수 있다. 이런 방법에는 half-adder 와 full-adder 가 존재하는데, half 의 경우는 두 비트만 더해서 carry와 sum을 출력 해주고 full 의 경우는 carry와 bit 두개를 모두 더한다.

다른 방법으로는 carry-ripple 방법이 있다. 이는 자릿수가 늘어나면 테이블의 입력을 늘리지 않고 적은 자릿수를 활용하는 여러 adder을 붙여서 제작하는 방법이다. 이 뜻은 아래와 같이 4자리, 4bit + 4bit의 연산을 할때에 1bit 끼리 더하는 circuit을 4개를 붙이고 carry 를 전 circuit에서 나오는 output carry를 input carry로 넣어주는 것이다. 이것이 물결치는 것과 비슷하여 ripple 이라고 한다.

또한 위처럼의 ripple adder는 4bit-adder, 4bit-adder, 초기 carry 가 입력으로 들어오고, 출력으로는 4bit의 값과 마지막 carry 값이 출력 된다.
하지만 이 방법은 다음 circuit을 계속 실행 시키기 위해서는 그 전의 carry output이 출력이 되어야 그 값이 들어가면서 실행될 수 있다.
따라서 계속해서 전 circuit 의 carry를 기다려야 하기 떄문에 시간이 오래 걸리게 되는 단점이 있다.
또한 계속해서 adder을 확장시키게 된다면 앞서의 원리와 같이 하위 bit 들을 합쳐서 더 큰 adder을 구현 시키면 된다.
multiply design by 3
3 * i 라면, i를 3번 더한 것과 그 결과가 같다고 할 수 있다. 이를 adder을 연결시켜서 만들어 낸다고 한다면 아래와 같이 표현 할 수 있다.

따라서 8bit 짜리에 3을 곱하게 된다면 10bit의 결과 값이 나오게 된다. 또, 이렇게 더하는 방법 대신에 짝수번곱하는 것은 shift 연산을 통하여 해결 할 수 있다. 곱하기는 shift 로 왼쪽으로 밀고, 나누기는 그 와 반대로 할 수 있다.
substraction using addition 이는 앞서 우리가 하였던 2의 보수를 이용하여 구현해 낼 수 있다.
따라서 x, y 에 대해 계산을 진행 할 때에 add 는 x + y 로 진행 할 수 있고, x - y 는 x + y' + 1 로 나타낼수 있다. 그 이유는 2의 보수를 사용한다면 -y = y' + 1로 나타낼 수 있기 때문이다. 따라서 이를 circuit으로 구현한다면 아래와 같이 나타낼 수 있다.
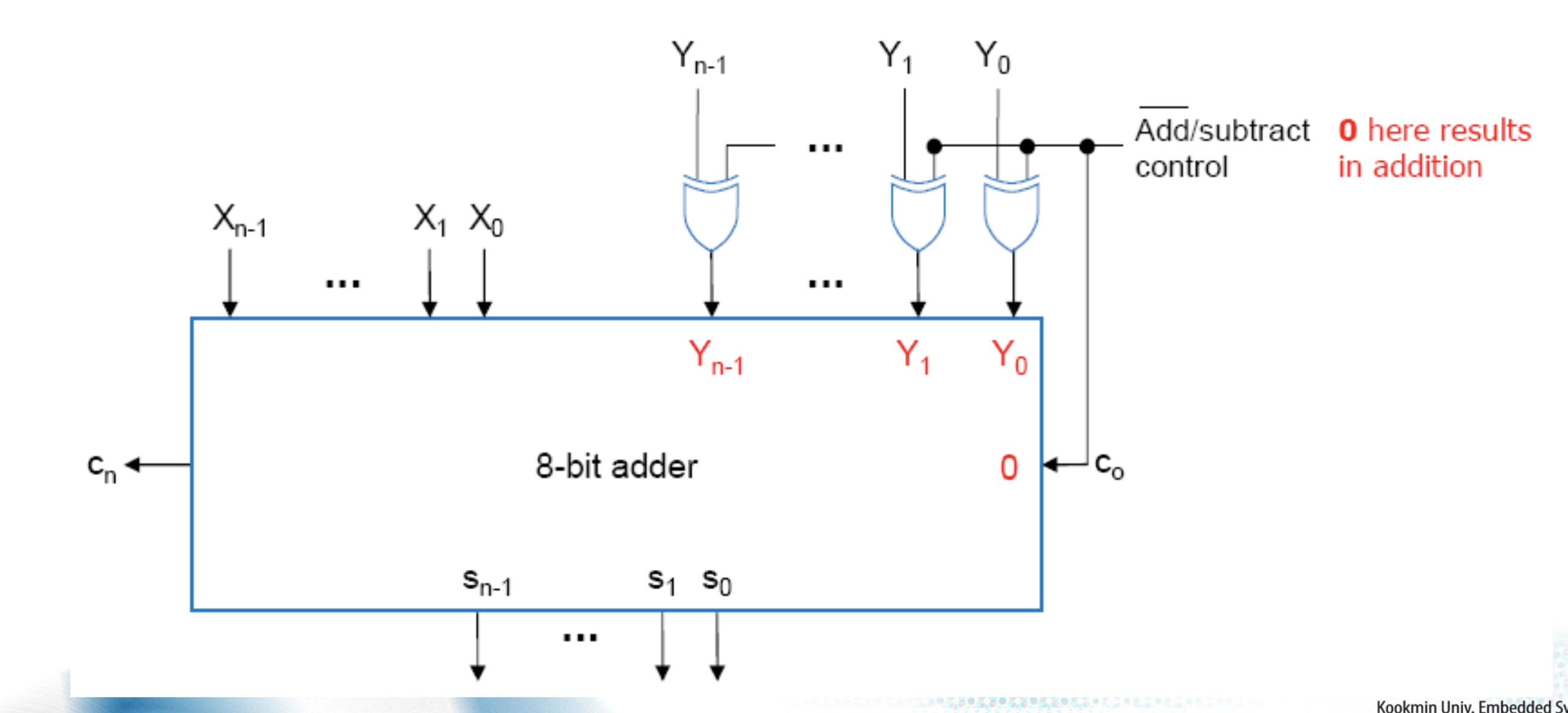
c0 에 0 이들어간다는 것은 y 가 양수라는 의미이기 때문에 변환하지 않고 그대로 하면 되고 음수 일때는 마지막에 1을 더해주어야 하므로 이를 신호로 보내주어서 1의 보수를 xor로 나타낸 후에 1을 더해주게 된다.
또한 이 여러 연산들을 진행 할 때에 나타낼 수 있는 비트수가 정해져 있기 때문에 unsigned 연산 ,모두가 양수일때하는 연산에서는 괜찮지만 음수가 있는 연산에서는 overflow 가 발생하면 이를 활용해야 옳은 값인지 아닌지를 판별해야 한다.

따라서 위의 그림을 토대로 생각한다면 올림수, carry가 서로 다를 때에는 overflow를 사용해야하고 양, 양을 더했을떄 음, 음 음을 더했을 때에 양수가 나온다면 overflow 를 활용해야한다는 의미로 해석할 수 있다.
또한 위에서 제기 했던 문제에서 carry-ripple 의 문제는 전의 carry 값을 기다려 야 한다는 것이 었는데 이를 look ahead, 미리 판단을 하여 시간을 줄일 수 있다.
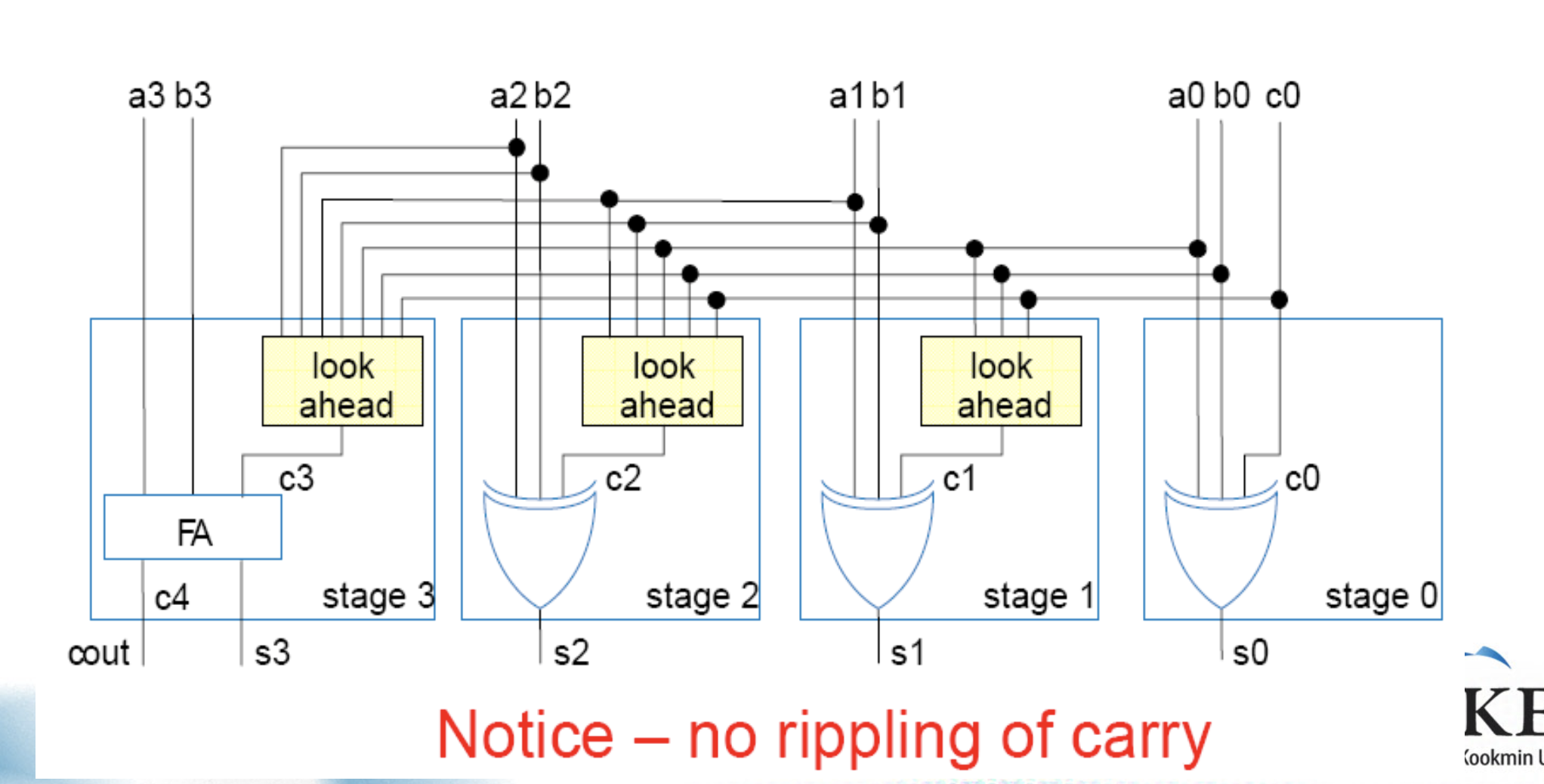
하지만, 이 또한 자릿수 가 증가할 수록, 끝자리의 look ahead circuit이 거대해 질 수 있다는 문제점이 존재한다.
'논리회로 설계' 카테고리의 다른 글
| Sequential circuit (0) | 2022.05.30 |
|---|---|
| 논회설 bit storage (0) | 2022.05.23 |
| mux & decoder (0) | 2022.05.16 |
| petrick method (0) | 2022.05.16 |
| 논리회로 설계 (0) | 2022.05.02 |