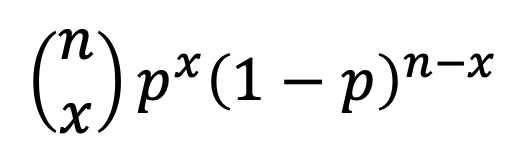하루에 하나씩 개발 공부

이항확률변수 : 베르누이 시행을 독립적으로 반복 시행하였을 때 나오는 성공의 횟수 이때의 베르누이는 겨로가 값이 두개인 시행을 뜻한다. 이항분포는 이항 확률변수의 분포이다. 이항분포의 n번의 시행에서 x 번 성공할 횟수는 아래와 같다, 총 n번 중에 x번 성공하고, 그에 대한 확률 성공시확률과 실패의 확률을 곱해준다. 누적 확률분포도 : 이항확률변수의 누적확률을 표로 정리한 것이다. 이때의 누적은 0부터 누적하는 것이다. 따라서 x < c 인 확률을 누적확률분포표를 통해서 구하려면, 1 - (0 < x) 인 확률이므로 P(0 < x) 인 확률을 누적확률분포표를 통해서 구한후에 1 에서 빼준다. 이항분포의 평균과 분산, 확률에서의 평균을 구하는 법은 확률변수에 그에 해당하는 확률을 곱하여 전체를 다 더하는..

추측통계학 : 표본에 내포되어있는 정보를 이용하여 모집단을 파악하는 것을 추측통계학이라고 한다. 이때에 중요한것은 추측을 얼마나 믿을 것인가 이다. 이때에 추론이 얼마나 정확한지를 따져주는 것을 확률이라고 한다. 확률이란 시행을 무한대로 하였을때에 어떠한 일이 일어나는 비율이다. 표본공간 : 모든 가능한 시행의 집합 사상 : 관심있는 실험결과들의 집합, 표본공간의 부분집합이다. 이때에 확률은 사상의 개수 / 표본공간의 원소의 개수 로 정의할 수 있다. 조합 - 조합은 경우의 수를 구하는데에 사용한다. 이 조합을 사용하는 경우는 비복원추출이나, 순서의 관계없이 뽑는경우에 활용할 수 있다. 확률의 덧셈법칙 : 합집합을 구할 때에 사용한다. 조건부 확률 : 특정 조건에서 일어날 확률이다. 이 조건부 확률은 교..

기술통계학 : 수집된 자료의 특성을 파악할 수 있도록 자료를 정리 추측통계학 : 표본으로 모집단을 추측 자료의 종류 : 양적 자료, 질적 자료 양적자료 : 숫자로 나타나는 자료들 질적자료 : 숫자로 표시할 수 없는 자료들 질적 자료의 해석 1.도수분포표 도수 : 각 자료값의 빈도수 상대도수 : 도수 / 전체 자료값 개수 이러한 상대도수를 표로 정리한 것을 도수분포표라고 한다 2. 양적자료해석 1.줄기 잎 표 2. 도수분포표 이는 우선 인접한 값들을 집단화한다. 계급폭 : max - min / 계급수 하측 경계 설정 : min 보다 작은 값으로 설정한다. 하측 경계로 부터 구간을 설정한다. 이렇게 만든 도수분포표를 막대로 나타내게디면 그것을 히스토그램이라고 한다. 이 히스토그램에서 처음 설정한 구간을 세분..