컴퓨터의 수의 수 체계는 2진수로 이루어져 있다.
따라서 2진수로 표현하고 더하고 빼는 여러 연산을 실행하게 되는데, 여기서 문제가 발생한다.
음수의 표현을 정하는 것인데, 이는 할당된 메모리의 맨 왼쪽의 비트를 부호 할당 비트로 지정하여 0은 양수 1은 음수로 약속을 한다.
따라서 이 방법을 사용하면 4비트가 주어진다면 맨 앞을 부호 할당을 위해 빼기 때문에 나타낼 수 있는 수는 -7 ~ +7 까지가 된다.
그런데 본인이 음수의 표현이 필요 없다면 맨 앞의 비트를 부호 할당을 위해 빼지 않아도 된다.
그러면 온전한 4비트를 사용가능하게 되어 0 ~ 15까지 총 16개의 수가 표현이 가능하다.
이러한 수 체계에도 문제가 발생하는데, 음수와 양수를 더하거나 음수와 음수를 더할때에 앞의 부호 할당자와 뒤의 magnitude number의 처리가 달라지기에 컴퓨터의 입장에서는 편하지 않은 처리 방식이 된다.
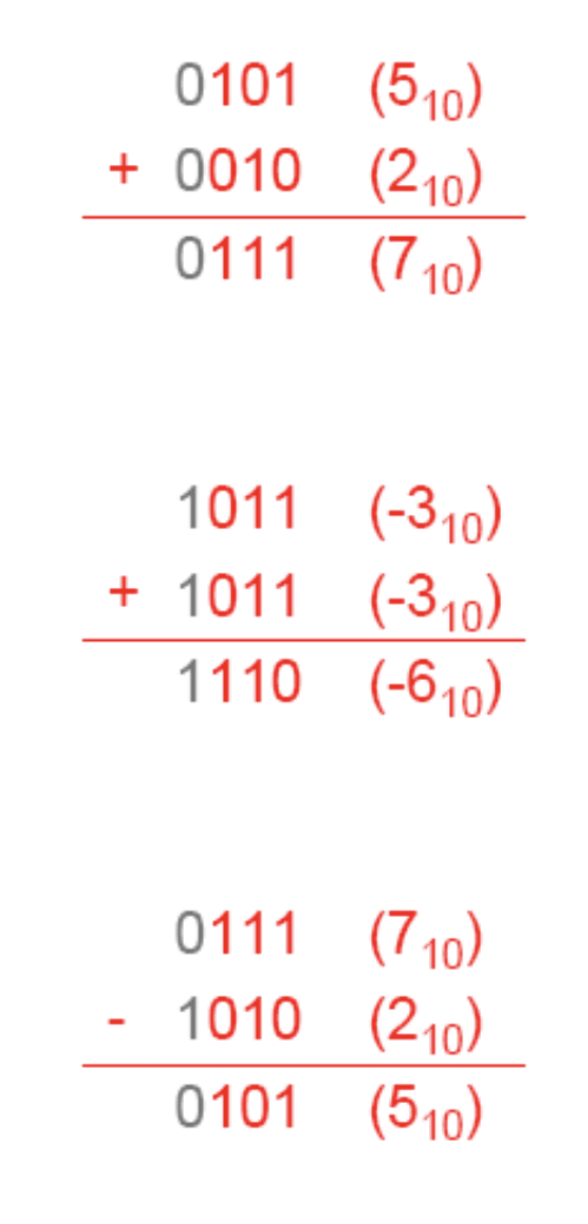
이를 개선 하기 위해 고안된 방법이 바로 2의 보수를 활용하는 방법이다. 2의 보수란 원래의 수 에서 무언가를 더해서 2를 만들게 하는 수 이다. 이러한 2의 보수를 만드는 방법은 우선 1의 보수를 먼저 쓴 후에 그 수에 1을 더하는 방식이다. 이렇게 만든 보수는 원래의 수의 음수가 된다. 그 이유는 원래의 수를 P 라하고 보수를 K라 하자.
이때 P + K = 2^n 이 된다. 이는 2진수로 나타내면 맨 앞자리만 1이고 뒷자리는 0이 되는데, 이에 맨 앞자리는 오버플로 이기 때문에 사용하지 않는다면, 최종적으로 0이된다. 따라서 P + K = 0 이 되므로 P = -K, 따라서 2진수에서의 2의 보수값을 음수로 약속할 수 있다.

위는 1의 보수를 사용하지 않고, 2의 보수를 사용하는 이유이다. 1의 보수를 사용하게 되면 오버플로가 발생하는지 확인 한 후에 오버플로를 제거 한 후에 발생한 경우 + 1을 해 주어야 한다. 이에 1의보수를 사용하여 1을 더하는 2이 보수를 사용하면 과정의 보완이되어 덧셈을 그냥 진행한 후에 오버플로만 제거 해 주면 된다.
정리하자면 , 수를 나타내는 방법은 3가지가 존재한다. Sign and magnitude, 1’s complement , 2’s complement 가 존재하는 데 오른쪽으로 갈 수록 보완이 된 방법이다. 각각의 문제는 Sign and magnitude는 작은 수에서 큰 수를 뺄 때에 큰 수 에서 작은 것을 뺀다음에 -를 붙여야 하고, 1의 보수는 각 계산마다 오버플로 가 발생하는지 체크한 후에 발생한 경우 1을 더해주어야 한다. 하지만 2의 보수의 경우는 그럴 필요없이 그냥 더하고 오버플로는 무시하면 된다. 따라서 2의 보수를 채택하여 활용한다.
'논리회로 설계' 카테고리의 다른 글
| 논리회로 설계 (0) | 2022.03.23 |
|---|---|
| 논리회로 설계 04 (0) | 2022.03.21 |
| 논리회로설계 (0) | 2022.03.16 |
| 논리회로 설계 (02) (0) | 2022.03.13 |
| 논리회로 설계 / 01 (0) | 2022.03.07 |