응용통계학 (검정 ~ 시계열)

1. 검정

검정이란 가설을 세운 후에 표본에 기초하여 가설을 채택하거나 기각하는 방식이다.

 

검정에서는 귀무가설(원래의 가설) 그에 대립하는 대립 가설을 세운다.

귀무가설의 경우는 모평균이나 예상하는 값이 표본의 그 값과 같다고 가정한다.

 

이때 두가지 오류가 존재하게 되는데, 제 1종오류와 제 2종오류가 있다. 

 

제1종 오류는 귀무가설이 참인데, 대립가설을 채택하는 경우이고 제 2종오류는 대립가설이 참인데, 귀무가설을 채택을 하는 오류이다.

 

이 둘을 동시에 관리할 수 는 없다 1종 오류를 줄이기 위해 유효 범위를 높이게 된다면, 2종오류의 가능성이 높아진다. 하지만, 반대의 경우는 1종오류의 확률이 높아진다.

 

이러한 표본에서의 검정은 두가지 케이스가 있다.

대표본에서의 검정과 소표본의 검정이 있다.

 

대표본에서의 검정

소표본에서의 검정

이때의 n은 표본의 개수이다.

 

모비율의 검정

 

 

모평균의 차의 검정

이때에도 두가지 경우가 있다. 대표본과 소표본일 때이다.

이때 대표본과 소표본을 나누는 기준은 n이 30이상이면 대표본, 아래이면 소표본이다. 

소표본일 경우

 

차이를 비교할때에 문제에서 두 집단의 평균이 한번에 구해져서 나오지 않고, 하나 하나 나오는 경우는 대응비교를 물어볼 확률이 높다.

대응 비교는 실험단위를 쌍으로 묶는다. 이때의 쌍으로 묶이는 수 들은 독립적인 추출이 아니다.

 

이때의 D는 쌍 안에서의 두 값의 차이 X1 - X2 이다. 이때 항상 양이 아니어도 된다.

이러한 대응 비교는 위에서 한 독립 비교보다 효과적이라고 할 수 있다. 

 

모비율의 차에 대한 검정

비모수적 검정 

 

비모수적 검정이란, 정규분포를 따르지 않을때 이다.

이때에 윌콕슨 순위합 검정을 사용한다. 이는 ㅗ평균의 차에대한 비모수적 검정이라고 생각해도 된다.

따라서 이떄의 귀무가설은 둘의 차이가 없다는 것이 귀무가설이다.

이때에도 소표본과 대표본으로 나누는데, 이때의 기준은 n 이 10이하이면 소표본에서의 검정을 진행한다. 

 

위에서의, W는 두 표본이 있을떄 개수가 적은 쪽의 순위합이다.

이떄에 E(W)에서 n2를 곱한 이유는 W가 두번째 표본이기 때문이다. 만약에 첫번쨰 표본이라면, n1을 곱해준다.

 

부호 순위검정 또한 있는데, 이는 표본의 집단이 하나 일때 사용한다. 이때의 귀무가설은 평균이 세타 이라는 것이다.

이때에 순위를 매길 때에 만일 값이 -이면 -를 붙여준다.

W+는 이렇게 붙인 순위들 중 양의 값들을 모두 더한것이다.

이떄에도 대표본이 있는데, 이떄의 기준은 10이 아닌, 15이다.

상관 분석과 회귀 분석

 

상관 분석은 두 변수가 서로 연관이 있는지 분석하는 것이다.  회귀분석은 두 변수 사이에서 함수관계를 찾는것이다.

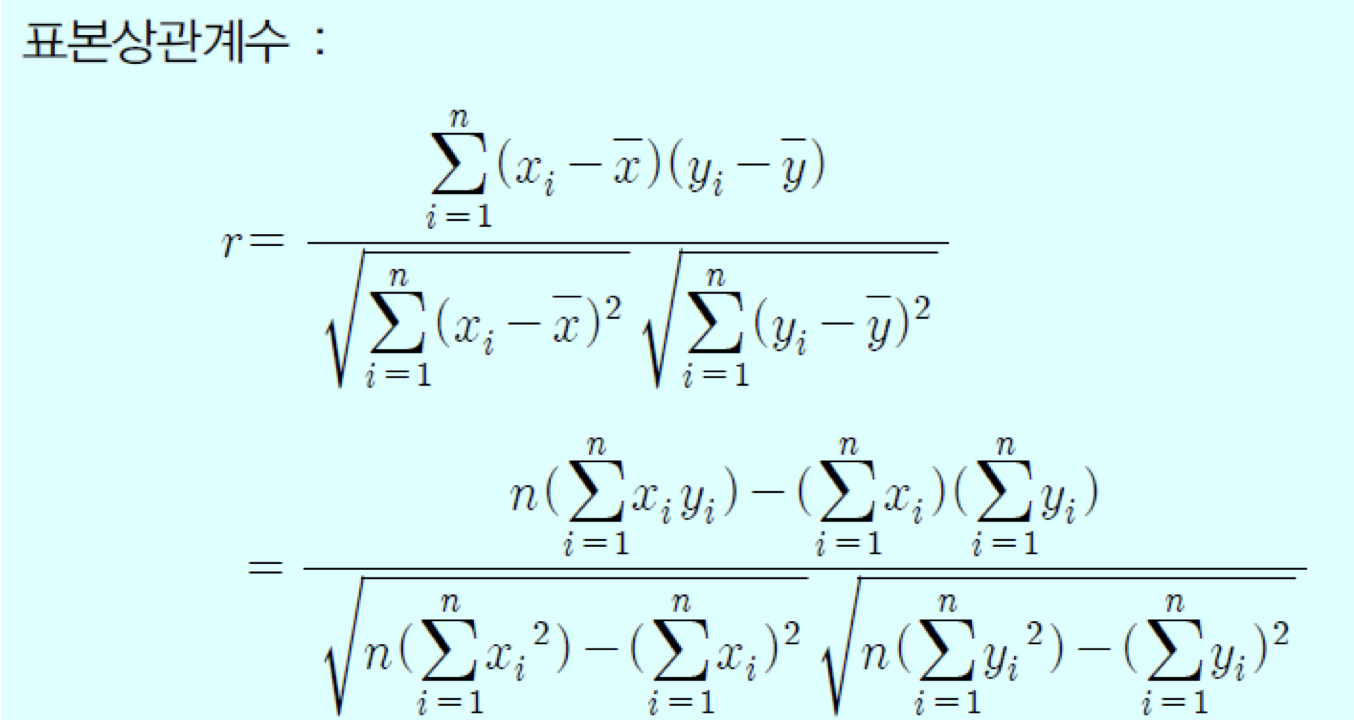
이를 보통 r 로 표현하는데 이 r 이 1에 가까워 질수록 양의 직선관계에 있다는 뜻이다. -1에 가까워지면 음의 직선관계에 있다는 의미이다.

하지만, 이 r이 1이나 -1에 가깝지 않다고 두 변수가 서로 관계가 없다는 뜻은 아니다. 곡선의 관계에 있을 수도 있기 때문이다.

 

이러한 상관계수를 표본으로 부터 구한 후에 검정을 거쳐야 한다. 이때의 귀무 가설은 모 상관계수가 0이라는 가설로 직선위에 있지 않다는 가설이다.

이때의 n은 x와 y의 개수를 모두 합친 값이 아닌, 그 쌍의 개수이다.

 

단순선형 회귀는 설명변수가 한개이고, 종속변수와 직선의 관계에 있닥 추론하는 경우다. 우리는 이 경우만을 다룬다.

회귀 분석 : 회귀 분석은 두 변수가 함수관계가 있다고 추론하는 것으로, 미지의 직선관계를 두고 추론한다.

이때 미지의 직선을 두면, 실제의 값과 차이가 난다. 이때 나는 차이를 평균이 0, 분산이 시그마인 정규 분포를 이룬다고 생각한다.

 

함수 또한 추론하는데, 이때 추론할 때에는 최대한 오차가 작도록 추론한다. 이를 최소제곱 추정값이라고 한다.

 

잔차 : 잔차란 위에서 뽑아낸 식에서의 y값과 실제 추정값의 차이를 뜻한다.

이 잔차의 제곱합을 잔차제곱합이라고 하며, SSE라고 표현한다.

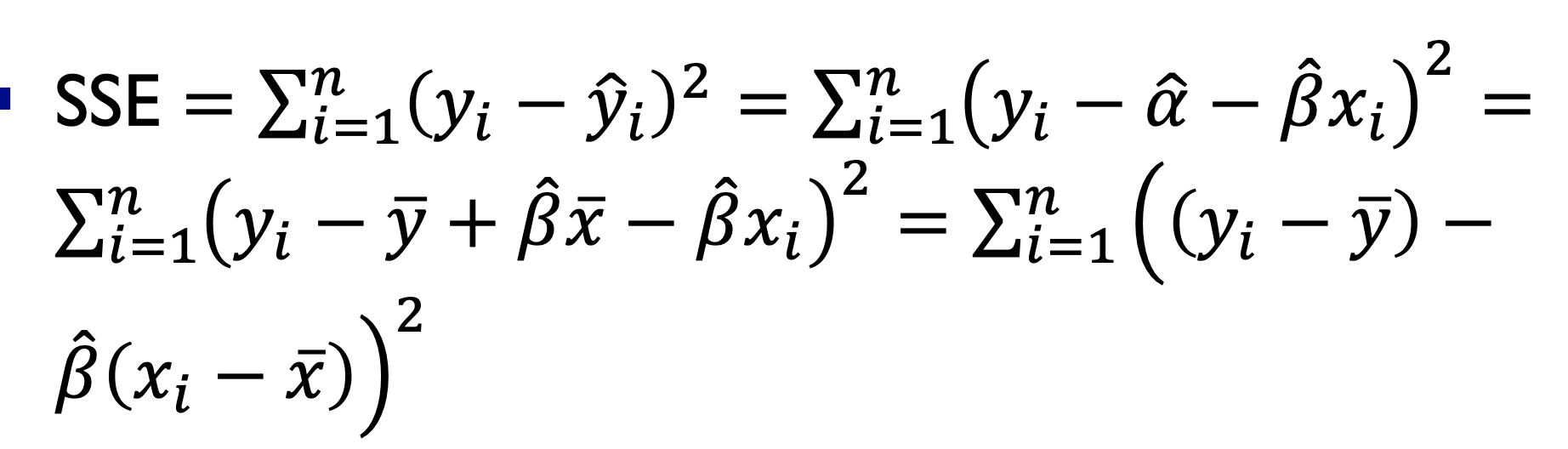
이를 통해 잔차들의 정규분포의 분산을 알 수 있는데, 

 

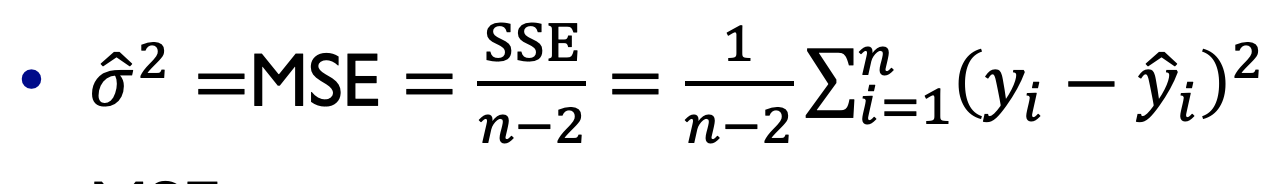
이때에 이 잔차 제곱합이 작을 수록 잘 근사된 식이라고 할 수 있는데, 얼마나 작은지를 알 수 없다. 

따라서 총 편차 제곱합에서의 차지 하는 비율이 작으면, 잘 근사 되었다고 할 수 있다. 

따라서 총편차 제곱합에서 잔차 제곱합을 뺸 수를 회귀 제곱합이라고 한다.

 

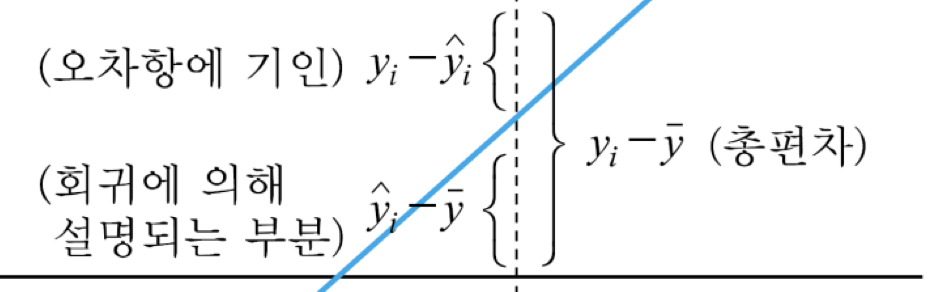
따라서 SSR의 값이 SST와 비슷하다면 좋다고 할 수 있는데, 이를 식으로 나타내면 SSR/SST이다. 이는 상관계수의 제곱과 같다.

 

 

ssr을 다르게 표현 할 수 도 있다 이때의 b는 직선의 기울기를 추정한 값이다.

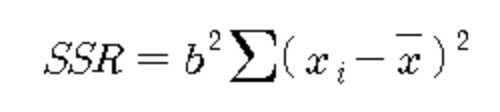
기울기를 구하고도 검정을 할 수 있는데, 다음을 따른다.

 

반응 편수의 평균값

알파 또한 검정 할 수 있는데, 위에 식에서 알파만, 넣어주면 된다.

 

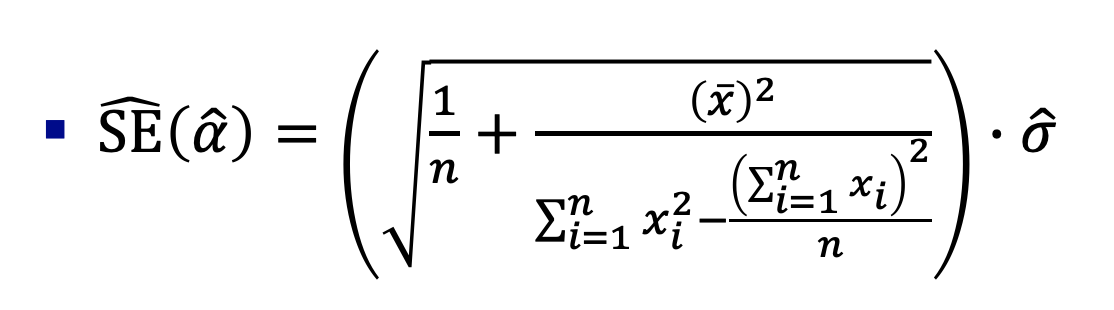
잔타 또한 검토해야 하는데, 잔차들이 0에 대해서 대칭이고, 특정한 형식이 없으면 된다.

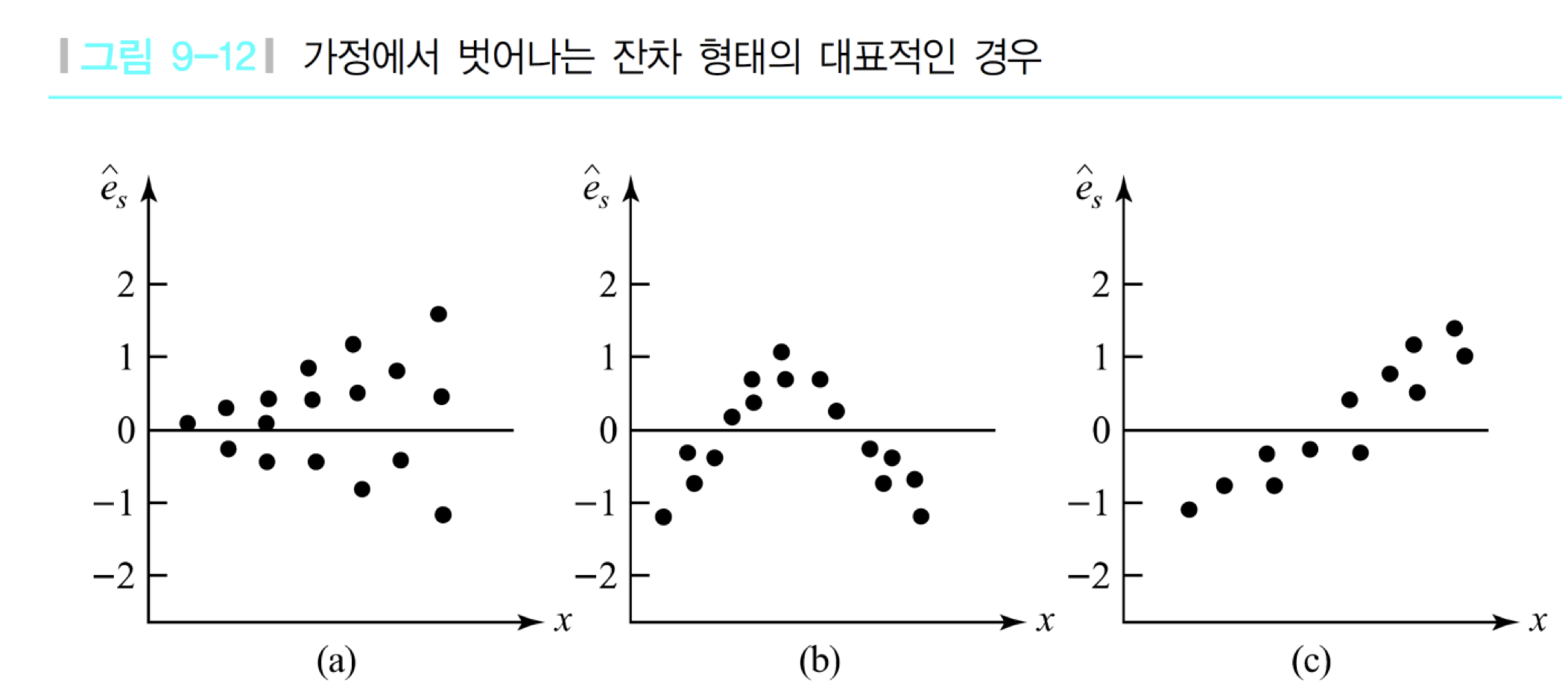
위 처럼 퍼져있으면 안 된다.

 

따라서 이제 회귀분석의 순서는 우선 관측값을 표시한 후 대략적인 관계를 파악한다. 그 후에 잔차를 검토한후, 결정계수를 구하여 직선관계에 있는지 확인한다. 그 후 직선을 추론하든 맘대로...

 

 

범주형 자료의 분석

 

이는 비율이 동일한지, 내가 기대하는 비율로 나오는지를 검정하는 것이다. 이를 카이제곱분포를 통해 검정한다.

 

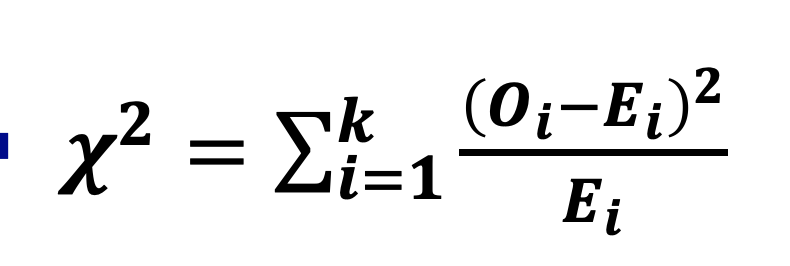
카이제곱 분포는 다음과 같다 .그리고 카이제곱은 제곱이기에 음수가 나오지 않는다. 따라서 임계값을 넘기면 기각 아니면 유지하는 케이스만 존재한다.

적합도 검정도 동일하게 진행한다.

 

독립성 검정과 동질성 검정 또한 있는데, 이 둘은 결과가 같다. 귀무 가설로는 두 결과가 독립이라는 가정하에 기댓값을 세운다. 따라서 귀무가설을 기각하게 되면 서로 독립이 아니라는 것이 된다.

 

일원 배치법

어떤 한 속성이 결과값에 영향을 미치는지를 알아보기 위한 검정이다. 

 

이때에 총편차, 수준간 편차, 수준내 편차를 구할 수 있는데, 총편차는 총 평균을 구한후 각각의 값들과의 편차, 수준간 편차는 각 수준의 대푯값인 평균과 전체 평균과의 편차, 수준내 편차는 각 수준안에서의 각 수준의 평균과의 편차이다.

 

이들을 각각 제곱합을 한다면, 

 

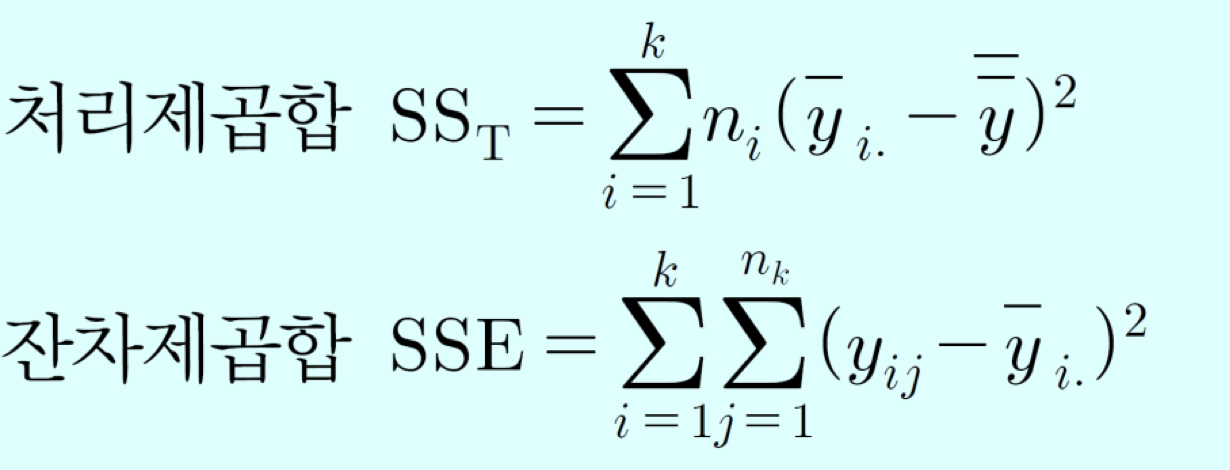
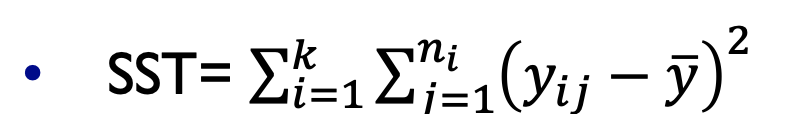
자유도도 각각 다르다

정리하면 아래와 같다.

 

시계열 시간의 경광 따라서 미래의 값을 예측하는 것이다. 

이때에 지수를 사용하는데, 지수는 특정 시의 값을 기준으로 각 시의 값들을 백분율로 나타낸 것이다. 

 

또한 추세를 파악하는데, 값이 들쭉 날 쭉이기 떄문에 평활법을 사용하기도 한다.

이동평균은 앞뒤에서 같은 수만큼 가져와 평균을 낸다. 짝수인 경우는 앞에 적은거 한번 뒤가 적은거 한번 평균을 내에 그 두개의 평균을 취한다.

 

지수 평활법은 가중ㅊ를 두어 계산하는 방식이다. 

미래 예측값은 마지막의 값을 평활법을 적용한 값이다. 

 

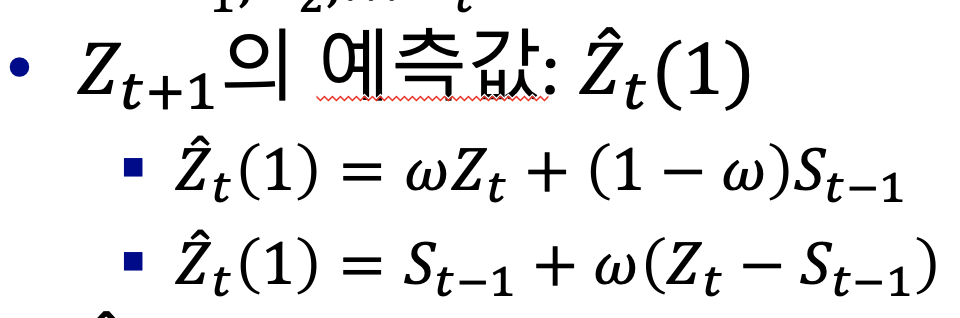
따라서 위표의 미래 예측값은 가장 마지막 값의 평활 값이다.