fp(컴퓨터 구조)

부동 소수점은 소수점이 떠서 돌아다닌다는 의미이다. 

이를 나타내는 식이 존재하는데, 다음과 같다.

fraction은 소수부를 뜻하고, exponent 는 지수부를 뜻한다.

single인 경우에는 exponent에 8bit, fraction에 23bit, 부호표현에 1bit 가 사용된다. 총 32bit

double인 경우에는 exponent에 11bit, fraction에 52bit, 부호표현에 1bit 가 사용된다. 총 64bit 이다.

 

bias 는 보통 127을 사용하는데, 그 이유는 지수부가 음수를 표현하지 않게 하기 위함이다. 따라서 -127을 함으로서 음수를 표현한다.

 

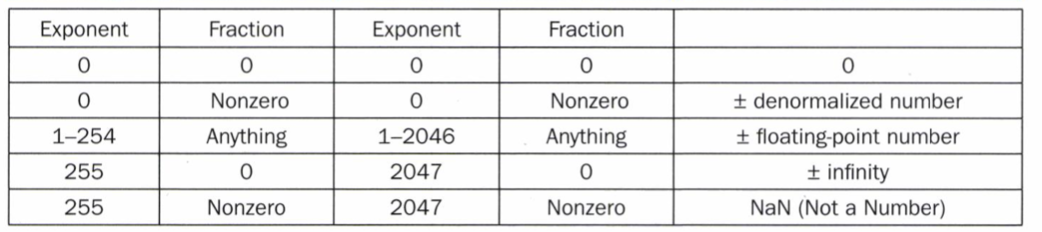
exponent 에는 예약 또한 걸려있는데, 아래와 같다.

 

십진수를 이진수로 나타내는 방법은 2로 나누면 된다. 그러면 십진수 소수를 이진수로 바꾸는 방법은 무엇일까? 바로 2를 곱하는 것이다.

 

이진수 소수표현을 십진수로 바꾸는 것은 거꾸로 진행하면 된다.

 

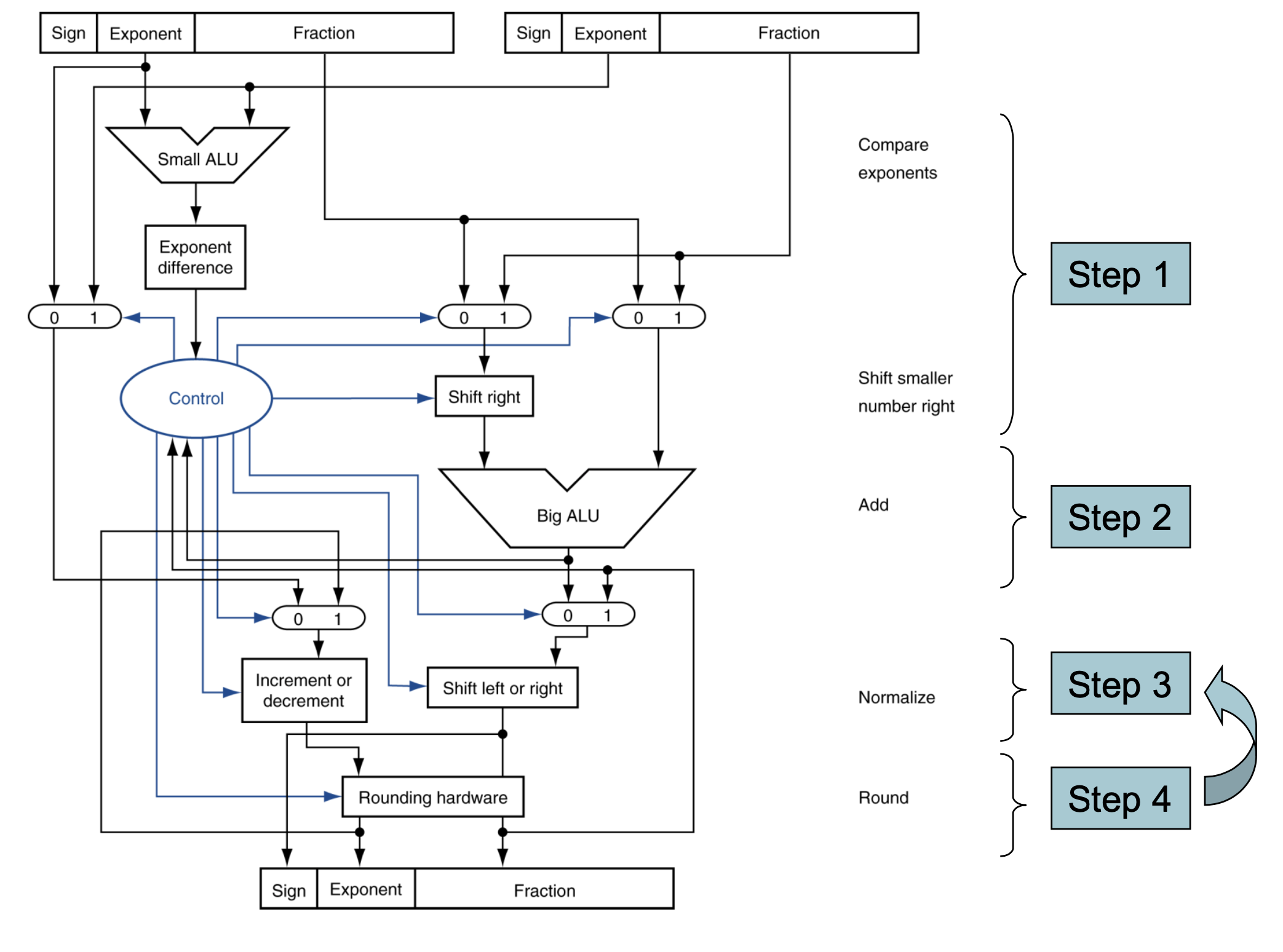
부동소수 덧셈하는 법

1. 먼저 작은 지수를 가지는 수의 소수점을 큰 지수와 같게 만들어야 한다.

(이때에 뒤에 늘어지는 수들은 자리수에 맞추어(23자리) 절사한다.)

2. 유효 자리를 더한다.

3. 다시 정돈한다.

4. 유효숫자에 맞게 반올림을 해준다.

 

이를 따라서 예를 들어 본다면, 9.999 * 10^1 + 1.610 * 10 ^ -1 을 유효숫자 4자리로 계산해보자.

우선 1.610 * 10 ^ -1의 지수부분을 10 ^ 1 로 만들어 주어야 한다.

따라서 1.610 * 10 ^ -1 * 10 ^ 2 * 10 ^ -2 = 0.0161 * 10 ^ 1 이다.

이제 유효숫자를 더하면, 0.0161 + 9.999 = 10.015이다.

이제 정돈하면 1.0015 * 10 ^ 2 로 나타낼 수 있고, 유효숫자가 4자리 이므로 1.002 * 10 ^ 2 로 나타낼수 있다.

 

이진수 일때엔 10을 2로만 바꾸면 된다. 

곱셈은 덧셈과 유사한데, 

1. 지수부를 더해준다. 이때 더해주는 이유는 곱셈이기 때문인데, 이때에 biased인지, unbiased인지에 따라서 다르다.

 

unbiased인 경우는 그냥 더해주면 된다. 하지만 biased인 경우에는 더해준 값에 127을 더해주어야 한다. 

그 이유는 예를 들어 -biased 된 값이 -1, -2이라면 원래의 수는 126, 125 이다. 따라서 곱한결과 의 biase된 값은 124이어야 하는데 그냥 더하게 된다면 -3 이다. 따라서 127을 더해주어야 한다. 

수식으로 쓴다면, (126 - 127) + (125 - 127) = 251 - 127 * 2 이므로 127은 한번만 빼면 되므로 반대로 127을 더해 주어야한다.

 

2. 그후에 곱셈을 진행하고 피연산자의 자리수 만큼 자른다.

 

3. 그 후 정규화를 진행하고, 유효숫자만큼 맞추어야 한다. 그리고 부호연산을 해준다.

 

 

이런 계산은 마지막에 정규화를 진행하기 때문에 정확한 연산이 될 수 없다. 따라서 float형 들을 계산 하는 경우에는 계산 순서에 따라서 결과 값이 달라진다.